2020年 AMC10 A卷

2020 AMC 10A Problems

Problem 1

What value of x satisfies

 

Problem 2

The numbers 3, 5, 7, a and b have an average (arithmetic mean) of 15. What is the average of a and b?

(A) 0 (B) 15 (C) 30 (D) 45 (E) 60

 

Problem 3

Assuming a ≠ 3, b ≠ 4, and c ≠ 5, what is the value in simplest form of the following expression?

(A) -1 (B) 1 (C)    (D)    (E)

 

Problem 4

A driver travels for 2 hours at 60 miles per hour, during which her car gets 30 miles per gallon of gasoline. She is paid $0.50 per mile, and her only expense is gasoline at $2.00 per gallon. What is her net rate of pay, in dollars per hour, after this expense?

(A) 20 (B) 22 (C) 24 (D) 25 (E) 26

 

Problem 5

What is the sum of all real numbers x for which 

(A) 12 (B) 15 (C) 18 (D) 21 (E) 25

 

Problem 6

How many 4-digit positive integers (that is, integers between 1000 and 9999, inclusive) having only even digits are divisible by 5

(A) 80 (B) 100 (C) 125 (D) 200 (E) 500

 

Problem 7

The 25 integers from -10 to 14, inclusive, can be arranged to form a 5-by-5 square in which the sum of the numbers in each row, the sum of the numbers in each column, and the sum of the numbers along each of the main diagonals are all the same. What is the value of this common sum?

(A) 2 (B) 5 (C) 10 (D) 25 (E) 50

 

Problem 8

What is the value of 1 + 2 + 3 - 4 + 5 + 6 + 7 - 8 + ... + 197 + 198 + 199 - 200 ?

(A) 9,800 (B) 9,900 (C) 10,000 (D) 10,100 (E) 10,200

 

Problem 9

A single bench section at a school event can hold either 7 adults or 11 children. When N bench sections are connected end to end, an equal number of adults and children seated together will occupy all the bench space. What is the least possible positive integer value of N?

(A) 9 (B) 18 (C) 27 (D) 36 (E) 77

 

Problem 10

Seven cubes, whose volumes are 1, 8, 27, 64, 125, 216, and 343 cubic units, are stacked vertically to form a tower in which the volumes of the cubes decrease from bottom to top. Except for the bottom cube, the bottom face of each cube lies completely on top of the cube below it. What is the total surface area of the tower (including the bottom) in square units?

(A) 644 (B) 658 (C) 664 (D) 720 (E) 749

 

Problem 11

What is the median of the following list of 4040 numbers?

1, 2, 3, ..., 2020, 12, 22, 32, ..., 20202

(A) 1974.5 (B) 1975.5 (C) 1976.5 (D) 1977.5 (E) 1978.5

 

Problem 12

Triangle AMC is isosceles with AM = AC. Medians  and  are perpendicular to each other, and MV = CU = 12. What is the area of ∆AMC ?

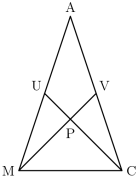
(A) 48 (B) 72 (C) 96 (D) 144 (E) 192

 

Problem 13

A frog sitting at the point (1, 2) begins a sequence of jumps, where each jump is parallel to one of the coordinate axes and has length 1, and the direction of each jump (up, down, right, or left) is chosen independently at random. The sequence ends when the frog reaches a side of the square with vertices (0, 0), (0, 4), (4, 4), and (4, 0). What is the probability that the sequence of jumps ends on a vertical side of the square?

 

Problem 14

Real numbers x and y satisfy x + y = 4 and x ∙ y = -2. What is the value of ?

(A) 360 (B) 400 (C) 420 (D) 440 (E) 480

 

Problem 15

A positive integer divisor of 12! is chosen at random. The probability that the divisor chosen is a perfect square can be expressed as , where m and n are relatively prime positive integers. What is m + n?

(A) 3 (B) 5 (C) 12 (D) 18 (E) 23

 

Problem 16

A point is chosen at random within the square in the coordinate plane whose vertices are (0, 0), (2020, 0), (2020, 2020), and  (0, 2020). The probability that the point is within d units of a lattice point is . (A point (x, y) is a lattice point if x and y are both integers.) What is d to the nearest tenth?

(A) 0.3 (B) 0.4 (C) 0.5 (D) 0.6 (E) 0.7

 

Problem 17

Define P(x) = (x - 12) (x - 22) ... (x - 1002). How many integers n are there such that P(n) ≤ 0 ?

(A) 4900 (B) 4950 (C) 5000 (D) 5050 (E) 5100

 

Problem 18

Let (a, b, c, d) be an ordered quadruple of not necessarily distinct integers, each one of them in the set 0, 1, 2, 3. For how many such quadruples is it true that a ∙ d - b ∙ c is odd? (For example, (0, 3, 1, 1) is one such quadruple, because 0 ∙ 1 - 3 ∙ 1 = -3 is odd.)

(A) 48 (B) 64 (C) 96 (D) 128 (E) 192

 

Problem 19

As shown in the figure below, a regular dodecahedron (the polyhedron consisting of 12 congruent regular pentagonal faces) floats in empty space with two horizontal faces. Note that there is a ring of five slanted faces adjacent to the top face, and a ring of five slanted faces adjacent to the bottom face. How many ways are there to move from the top face to the bottom face via a sequence of adjacent faces so that each face is visited at most once and moves are not permitted from the bottom ring to the top ring?

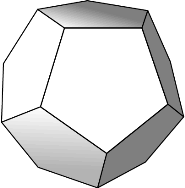
(A) 125 (B) 250 (C) 405 (D) 640 (E) 810

 

Problem 20

Quadrilateral ABCD satisfies ∠ABC = ∠ACD = 90°, AC = 20, and CD = 30. Diagonals  and  intersect at point E, and AE = 5. What is the area of quadrilateral ABCD?

(A) 330 (B) 340 (C) 350 (D) 360 (E) 370

 

Problem 21

There exists a unique strictly increasing sequence of nonnegative integers a1 < a2 < ... < ak  such that . What is k?

(A) 117 (B) 136 (C) 137 (D) 273 (E) 306

 

 

Problem 22

For how many positive integers n ≤ 1000  is  not divisible by 3? (Recall that  is the greatest integer less than or equal to x.)

(A) 22 (B) 23 (C) 24 (D) 25 (E) 26

 

Problem 23

Let T be the triangle in the coordinate plane with vertices (0, 0), (4, 0), and (0, 3). Consider the following five isometries (rigid transformations) of the plane: rotations of 90°, 180° and 270° counterclockwise around the origin, reflection across the x-axis, and reflection across the y-axis. How many of the 125 sequences of three of these transformations (not necessarily distinct) will return T to its original position? (For example, a 180° rotation, followed by a reflection across the x-axis, followed by a reflection across the y-axis will return T to its original position, but a 90° rotation, followed by a reflection across the x-axis, followed by another reflection across the x-axis will not return T to its original position.)

(A) 12 (B) 15 (C) 17 (D) 20 (E) 25

 

 

Problem 24

Let n be the least positive integer greater than 1000 for which gcd(63, n + 120) = 21 and gcd(n + 63, 120) = 60. What is the sum of the digits of n?

(A) 12 (B) 15 (C) 18 (D) 21 (E) 24

 

Problem 25

Jason rolls three fair standard six-sided dice. Then he looks at the rolls and chooses a subset of the dice (possibly empty, possibly all three dice) to reroll. After rerolling, he wins if and only if the sum of the numbers face up on the three dice is exactly 7. Jason always plays to optimize his chances of winning. What is the probability that he chooses to reroll exactly two of the dice?