2015年 AMC12 A卷

2015 AMC 12A Problems

Problem 1

What is the value of (20 - 1 + 52 - 0)-1 x 5?

$\textbf{(A)}\ -125\qquad\textbf{(B)}\ -120\qquad\textbf{(C)}\ \frac{1}{5}\qquad\textbf{(D)}\ \frac{5}{24}\qquad\textbf{(E)}\ 25$

Problem 2

Two of the three sides of a triangle are 20 and 15. Which of the following numbers is not a possible perimeter of the triangle?

$\textbf{(A)}\ 52\qquad\textbf{(B)}\ 57\qquad\textbf{(C)}\ 62\qquad\textbf{(D)}\ 67\qquad\textbf{(E)}\ 72$

Problem 3

Mr. Patrick teaches math to 15 students. He was grading tests and found that when he graded everyone's test except Payton's, the average grade for the class was 80. After he graded Payton's test, the class average became 81. What was Payton's score on the test?

$\textbf{(A)}\ 81\qquad\textbf{(B)}\ 85\qquad\textbf{(C)}\ 91\qquad\textbf{(D)}\ 94\qquad\textbf{(E)}\ 95$

Problem 4

The sum of two positive numbers is 5 times their difference. What is the ratio of the larger number to the smaller?

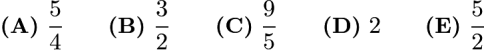
$\textbf{(A)}\ \frac54 \qquad\textbf{(B)}\ \frac32 \qquad\textbf{(C)}\ \frac95 \qquad\textbf{(D)}\ 2 \qquad\textbf{(E)}\ \frac52$

Problem 5

Amelia needs to estimate the quantity , where a, b and c are large positive integers. She rounds each of the integers so that the calculation will be easier to do mentally. In which of these situations will her answer necessarily be greater than the exact value of ?

(A) She rounds all three numbers up.

(B) She rounds a and b up,and she rounds c down.

(D) She rounds a up, and she rounds b and c down.

(E) She rounds c up, and she rounds a and b down.

Problem 6

Two years ago Pete was three times as old as his cousin Claire. Two years before that, Pete was four times as old as Claire. In how many years will the ratio of their ages be 2 : 1 ?

$\textbf{(A)}\ 2 \qquad\textbf{(B)}\ 4 \qquad\textbf{(C)}\ 5 \qquad\textbf{(D)}\ 6 \qquad\textbf{(E)}\ 8$

Problem 7

Two right circular cylinders have the same volume. The radius of the second cylinder is 10% more than the radius of the first. What is the relationship between the heights of the two cylinders?

(A) The second height is 10% less than the first.

(B) The first height is 10% more than the second.

(D) The first height is 21% more than the second.

(E) The second height is 80% of the first.

Problem 8

The ratio of the length to the width of a rectangle is 4 : 3. If the rectangle has diagonal of length d, then the area may be expressed as kd2 for some constant k. What is k ?

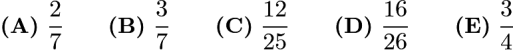
$\textbf{(A)}\ \frac27 \qquad\textbf{(B)}\ \frac37 \qquad\textbf{(C)}\ \frac{12}{25} \qquad\textbf{(D)}\ \frac{16}{26} \qquad\textbf{(E)}\ \frac34$

Problem 9

A box contains 2 red marbles, 2 green marbles, and 2 yellow marbles. Carol takes 2 marbles from the box at random; then Claudia takes 2 of the remaining marbles at random; and then Cheryl takes the last 2 marbles. What is the probability that Cheryl gets 2 marbles of the same color?

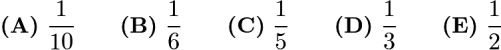
$\textbf{(A)}\ \frac{1}{10} \qquad\textbf{(B)}\ \frac16 \qquad\textbf{(C)}\ \frac15 \qquad\textbf{(D)}\ \frac13 \qquad\textbf{(E)}\ \frac12$

Problem 10

Integers x and y with x > y > 0 satisfy x + y + xy = 80. What is x?

$\textbf{(A)}\ 8 \qquad\textbf{(B)}\ 10 \qquad\textbf{(C)}\ 15 \qquad\textbf{(D)}\ 18 \qquad\textbf{(E)}\ 26$

Problem 11

On a sheet of paper, Isabella draws a circle of radius 2, a circle of radius 3, and all possible lines simultaneously tangent to both circles. Isabella notices that she has drawn exactly k ≥ 0 lines. How many different values of k are possible?

$\textbf{(A)}\ 2 \qquad\textbf{(B)}\ 3 \qquad\textbf{(C)}\ 4 \qquad\textbf{(D)}\ 5\qquad\textbf{(E)}\ 6$

Problem 12

The parabolas y = ax2 -2 and y = 4 - bx2 intersect the coordinate axes in exactly four points, and these four points are the vertices of a kite of area 12. What is a + b?

$\textbf{(A)}\ 1\qquad\textbf{(B)}\ 1.5\qquad\textbf{(C)}\ 2\qquad\textbf{(D)}\ 2.5\qquad\textbf{(E)}\ 3$

Problem 13

A league with 12 teams holds a round-robin tournament, with each team playing every other team exactly once. Games either end with one team victorious or else end in a draw. A team scores 2 points for every game it wins and 1 point for every game it draws. Which of the following is NOT a true statement about the list of 12 scores?

(A) There must be an even number of odd scores.

(B) There must be an even number of even scores.

(D) The sum of the scores must be at least 100.

(E) The highest score must be at least 12.

Problem 14

What is the value of a for which ?

$\textbf{(A)}\ 9\qquad\textbf{(B)}\ 12\qquad\textbf{(C)}\ 18\qquad\textbf{(D)}\ 24\qquad\textbf{(E)}\ 36$

Problem 15

$\frac{123456789}{2^{26}\cdot 5^4}$ What is the minimum number of digits to the right of the decimal point needed to express the fraction as a decimal?

$\textbf{(A)}\ 4\qquad\textbf{(B)}\ 22\qquad\textbf{(C)}\ 26\qquad\textbf{(D)}\ 30\qquad\textbf{(E)}\ 104$

Problem 16

Tetrahedron ABCD has AB = 5, AC = 3, BC = 4, BD = 4, AD = 3, and . What is the volume of the tetrahedron?

$\textbf{(A)}\ 3\sqrt{2}\qquad\textbf{(B)}\ 2\sqrt{5}\qquad\textbf{(C)}\ \frac{24}{5}\qquad\textbf{(D)}\ 3\sqrt{3}\qquad\textbf{(E)}\ \frac{24}{5}\sqrt{2}$

Problem 17

Eight people are sitting around a circular table, each holding a fair coin. All eight people flip their coins and those who flip heads stand while those who flip tails remain seated. What is the probability that no two adjacent people will stand?

$\textbf{(A)}\ \frac{47}{256} \qquad\textbf{(B)}\ \frac{3}{16} \qquad\textbf{(C)}\ \frac{49}{256} \qquad\textbf{(D)}\ \frac{25}{128} \qquad\textbf{(E)}\ \frac{51}{256}$

Problem 18

The zeros of the function f(x) = x2 - ax + 2a are integers. What is the sum of the possible values of a?

$\textbf{(A)}\ 7 \qquad\textbf{(B)}\ 8 \qquad\textbf{(C)}\ 16 \qquad\textbf{(D)}\ 17 \qquad\textbf{(E)}\ 18$

Problem 19

For some positive integers p, there is a quadrilateral ABCD with positive integer side lengths, perimeter p, right angles at B and C, AB = 2, and CD = AD. How many different values of p < 2015 are possible?

$\textbf{(A)}\ 30 \qquad\textbf{(B)}\ 31 \qquad\textbf{(C)}\ 61 \qquad\textbf{(D)}\ 62 \qquad\textbf{(E)}\ 63$

Problem 20

Isosceles triangles T and T′ are not congruent but have the same area and the same perimeter. The sides of T have lengths of 5, 5 and 8, while those of T′ have lengths of a, a and b. Which of the following numbers is closest to b?

$\textbf{(A)}\ 3 \qquad\textbf{(B)}\ 4 \qquad\textbf{(C)}\ 5 \qquad\textbf{(D)}\ 6 \qquad\textbf{(E)}\ 8$

Problem 21

A circle of radius r passes through both foci of, and exactly four points on, the ellipse with equation x2 + 16y2 = 16. The set of all possible values of r is an interval (a,b). What is a + b?

$\textbf{(A)}\ 5\sqrt{2}+4 \qquad\textbf{(B)}\ \sqrt{17}+7 \qquad\textbf{(C)}\ 6\sqrt{2}+3 \qquad\textbf{(D)}\ \sqrt{15}+8 \qquad\textbf{(E)}\ 12$

Problem 22

For each positive integer n, let S(n) be the number of sequences of length n consisting solely of the letters A and B, with no more than three As in a row and no more than three Bs in a row. What is the remainder when S(2015) is divided by 12?

$\textbf{(A)}\ 0 \qquad\textbf{(B)}\ 4 \qquad\textbf{(C)}\ 6 \qquad\textbf{(D)}\ 8 \qquad\textbf{(E)}\ 10$

Problem 23

Let S be a square of side length 1. Two points are chosen independently at random on the sides of S. The probability that the straight-line distance between the points is at least is , where a,b and c are positive integers and gcd(a,b,c) = 1. What is a + b + c?

$\textbf{(A)}\ 59 \qquad\textbf{(B)}\ 60 \qquad\textbf{(C)}\ 61 \qquad\textbf{(D)}\ 62 \qquad\textbf{(E)}\ 63$

Problem 24

Rational numbers a and b are chosen at random among all rational numbers in the interval (0,2) that can be written as fractions where n and d are integers with 1 ≤ d ≤ 5. What is the probability that (cos(aπ) + isin(bπ))4 is a real number?

$\textbf{(A)}\ \frac{3}{50} \qquad\textbf{(B)}\ \frac{4}{25} \qquad\textbf{(C)}\ \frac{41}{200} \qquad\textbf{(D)}\ \frac{6}{25} \qquad\textbf{(E)}\ \frac{13}{50}$

Problem 25

A collection of circles in the upper half-plane, all tangent to the x-axis, is constructed in layers as follows. Layer L0 consists of two circles of radii 702 and 732 that are externally tangent. For k ≥ 1, the circles in are ordered according to their points of tangency with the x-axis. For every pair of consecutive circles in this order, a new circle is constructed externally tangent to each of the two circles in the pair. Layer Lk consists of the 2k-1 circles constructed in this way. Let , and for every circle C denote by r(C) its radius. What is ?

$[asy] import olympiad; size(350); defaultpen(linewidth(0.7)); // define a bunch of arrays and starting points pair[] coord = new pair[65]; int[] trav = {32,16,8,4,2,1}; coord[0] = (0,73^2); coord[64] = (2*73*70,70^2); // draw the big circles and the bottom line path arc1 = arc(coord[0],coord[0].y,260,360); path arc2 = arc(coord[64],coord[64].y,175,280); fill((coord[0].x-910,coord[0].y)--arc1--cycle,gray(0.75)); fill((coord[64].x+870,coord[64].y+425)--arc2--cycle,gray(0.75)); draw(arc1^^arc2); draw((-930,0)--(70^2+73^2+850,0)); // We now apply the findCenter function 63 times to get // the location of the centers of all 63 constructed circles. // The complicated array setup ensures that all the circles // will be taken in the right order for(int i = 0;i<=5;i=i+1) { int skip = trav[i]; for(int k=skip;k<=64 - skip; k = k + 2*skip) { pair cent1 = coord[k-skip], cent2 = coord[k+skip]; real r1 = cent1.y, r2 = cent2.y, rn=r1*r2/((sqrt(r1)+sqrt(r2))^2); real shiftx = cent1.x + sqrt(4*r1*rn); coord[k] = (shiftx,rn); } // Draw the remaining 63 circles } for(int i=1;i<=63;i=i+1) { filldraw(circle(coord[i],coord[i].y),gray(0.75)); } [/asy]$
$\textbf{(A)}\ \frac{286}{35} \qquad\textbf{(B)}\ \frac{583}{70} \qquad\textbf{(C)}\ \frac{715}{73}\qquad\textbf{(D)}\ \frac{143}{14} \qquad\textbf{(E)}\ \frac{1573}{146}$