COMC 2014年真题

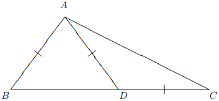
A1.In triangle ABC, there is a point D on side BC such that BA = AD = DC. Suppose ∠BAD = 80°. Determine the size of ∠ACB.

A2.The equations x2 − a = 0 and 3x4 − 48 = 0 have the same real solutions. What is the value of a?

A3.A positive integer m has the property that when multiplied by 12, the result is a four-digit number n of the form 20A2 for some digit A. What is the 4 digit number, n?

A4.Alana, Beatrix, Celine, and Deanna played 6 games of tennis together. In each game, the four of them split into two teams of two and one of the teams won the game. If Alana was

on the winning team for 5 games, Beatrix for 2 games, and Celine for 1 game, for how many games was Deanna on the winning team?

B1.The area of the circle that passes through the points (1, 1),(1, 7), and (9, 1) can be expressed as kπ. What is the value of k?

B2.Determine all integer values of n for which n2 + 6n + 24 is a perfect square.

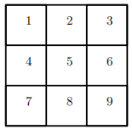
B3.5 Xs and 4 Os are arranged in the below grid such that each number is covered by either an X or an O. There are a total of 126 different ways that the Xs and Os can be placed. Of these

126 ways, how many of them contain a line of 3 Os and no line of 3 Xs?

A line of 3 in a row can be a horizontal line, a vertical line, or one of the diagonal lines 1−5−9 or 7 − 5 − 3.

B4.Let . Determine the smallest positive integer n such that

C1.A sequence of the form {t1, t2, ..., tn} is called geometric

if t1 = a, t2 = ar, t3 = ar2, ... , tn = arn−1. For example, {1, 2, 4, 8, 16} and {1, −3, 9, −27} are both geometric sequences. In all

three questions below, suppose {t1, t2, t3, t4, t5} is a geometric sequence of real numbers.

(a) If t1 = 3 and t2 = 6, determine the value of t5.

(b) If t2 = 2 and t4 = 8, determine all possible values of t5.

C2.The line L given by 5y + (2m − 4)x − 10m = 0 in the

xy-plane intersects the rectangle with vertices O(0, 0), A(0

, 6), B(10, 6), C(10, 0) at D on the line segment OA and E

on the line segment BC.

(a) Show that 1 ≤ m ≤ 3.

(b) Show that the area of quadrilateral ADEB is the area of rectangle OABC.

L that intersects OA at F and BC at G so that the quadrilaterals

ADEB, DEGF, F GCO all have the same area.

C3.A local high school math club has 12 students in it. Each week, 6 of the students go on a field trip.

(a) Jeffrey, a student in the math club, has been on a trip with each other student in the math club. Determine the minimum number of trips that Jeffrey could have gone on.

(b) If each pair of students have been on at least one field trip together, determine the minimum number of field trips that could have happened

C4.A polynomial f(x) with real coefficients is said to be a sum of squares if there are polynomials p1(x), p2(x),...,pn(x) with real coefficients for which

For example, 2x4 + 6x2 − 4x + 5 is a sum of squares because

(a) Determine all values of a for which f(x) = x2 + 4x + a is a sum of squares.

(b) Determine all values of a for which f(x) = x4 + 2x3 + (a − 7)x2 + (4 − 2a)x + a is a sum of squares, and for such values of a, write f(x) as a sum of squares.