COMC 2019年真题

A1.Shawn’s password to unlock his phone is four digits long, made up of two 5s and two 3s. How many different possibilities are there for Shawn’s password?

A2.Triangle ABC has integer side lengths and perimeter 7. Determine all possible lengths of side AB.

A3.If a and b are positive integers such that a = 0.6 b and gcd(a, b) = 7, find a + b.

A4.The equations and x4 - ax2 + 4 = 0 have the same roots. Determine the value of a.

B1.John walks from home to school with a constant speed, and his sister Joan bikes twice as fast. The distance between their home and school is 3 km. If Joan leaves home 15 minutes after John then they arrive to school at the same time. What is the walking speed (in km/h) of John?

B2.What is the largest integer n such that the quantity

is an integer?

Note: Here k! = 1 × 2 × 3 × · · · × k is the product of all integers from 1 to k. For example, 4! = 1 × 2 × 3 × 4 = 24.

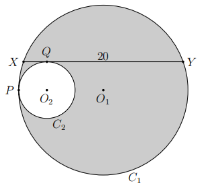
B3.In the diagram below circles C1 and C2 have centres O1 and O2. The radii of the circles are respectively r1 and r2 with r1 = 3r2. C2 is internally tangent to C1 at P. Chord XY of C1 has length 20, is tangent to C2 at Q and is parallel to O2O1. Determine the area of the shaded region: that is, the region inside C1 but not C2.

B4.Bob and Jane hold identical decks of twelve cards, three of each colour: red, green, yellow, and blue. Bob and Jane shuffle their decks and then take turns dealing one card at a time onto a pile, with Jane going first. Find the probability that Jane deals all her red cards before Bob deals any of his red cards.

Give your answer in the form of a fraction in lowest terms.

C1.The function f is defined on the natural numbers 1, 2, 3, . . . by f(1) = 1 and

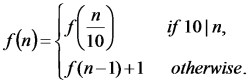
Note: The notation b | a means integer number a is divisible by integer number b.

(a) Calculate f(2019).

(b) Determine the maximum value of f(n) for n ≤ 2019.

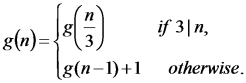
Determine the maximum value of g(n) for n ≤ 100.

C2.(a) Let ABCD be an isosceles trapezoid with AB = CD = 5, BC = 2, AD = 8. Find the height of the trapezoid and the length of its diagonals.

(b) For the trapezoid introduced in (a), find the exact value of cos ∠ABC.

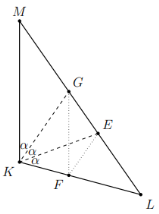
(c) In triangle KLM, let points G and E be on segment LM so that ∠MKG = ∠GKE = ∠EKL = α. Let point F be on segment KL so that GF is parallel to KM. Given that KF EG is an isosceles trapezoid and that ∠KLM = 84° , determine α.

C3.Let N be a positive integer. A “good division of N” is a partition of {1, 2, . . . , N} into two disjoint non-empty subsets S1 and S2 such that the sum of the numbers in S1 equals the

product of the numbers in S2. For example, if N = 5, then

S1 = {3, 5}, S2 = {1, 2, 4}

would be a good division.

(a) Find a good division of N = 7.

(b) Find an N which admits two distinct good divisions.

C4.Three players A, B and C sit around a circle to play a game in the order A → B → C → A → · · · . On their turn, if a player has an even number of coins, they pass half of them to the next player and keep the other half. If they have an odd number, they discard 1 and keep the rest. For example, if players A, B and C start with (2, 3, 1) coins, respectively, then

they will have (1, 4, 1) after A moves, (1, 2, 3) after B moves, and (1, 2, 2) after C moves, etc. (Here underline indicates the player whose turn is next to move.) We call a position (x, y, z)