2019 AIME I 真题

Problem 2

Jenn randomly chooses a number J from 1, 2, 3, ..., 19, 20. Bela then randomly chooses a number B from 1, 2, 3, ..., 19, 20 distinct from J. The value of B - J is at least 2 with a probability that can be expressed in the form , where m and n are relatively prime positive integers. Find m + n.

Problem 3

In ∆PQR, PR = 15, QR = 20, and PQ = 25. Points A and B lie on , points C and D lie on , and points E and F lie on , with PA = QB = QC = RD = RE = PF = 5. Find the area of hexagon ABCDEF.

Problem 4

A soccer team has 22 available players. A fixed set of 11 players starts the game, while the other 11 are available as substitutes. During the game, the coach may make as many as 3 substitutions, where any one of the 11 players in the game is replaced by one of the substitutes. No player removed from the game may reenter the game, although a substitute entering the game may be replaced later. No two substitutions can happen at the same time. The players involved and the order of the substitutions matter. Let n be the number of ways the coach can make substitutions during the game (including the possibility of making no substitutions). Find the remainder when n is divided by 1000.

Problem 5

A moving particle starts at the point (4, 4) and moves until it hits one of the coordinate axes for the first time. When the particle is at the point (a, b), it moves at random to one of the points (a - 1, b), (a, b - 1), or (a - 1, b - 1), each with probability , independently of its previous moves. The probability that it will hit the coordinate axes at (0, 0) is , where m and n are positive integers, and m is not divisible by 3. Find m +n.

Problem 6

In convex quadrilateral KLMN, side  is perpendicular to diagonal , side  is perpendicular to diagonal , MN = 65, and KL = 28. The line through L perpendicular to side  intersects diagonal  at  with KO = 8. Find MO.

Problem 7

There are positive integers x and y that satisfy the system of equations log10 x + 2log10(gcd(x, y)) = 60log10 y + 2log10(lcm(x,y)) = 570. Let m be the number of (not necessarily distinct) prime factors in the prime factorization of x, and let  be the number of (not necessarily distinct) prime factors in the prime factorization of y. Find 3m + 2n.

Problem 8

Let x be a real number such that . Then  where m and n are relatively prime positive integers. Find m + n.

Problem 9

Let  denote the number of positive integer divisors of n. Find the sum of the six least positive integers n that are solutions to .

Problem 10

For distinct complex numbers z1, z2, ..., z673, the polynomial (x -z1)3(x - z2)3 ... (x - z673)3 can be expressed as x2019 + 20x2018 + 19x2017 + g(x), where g(x) is a polynomial with complex coefficients and with degree at most 2016. The value of 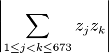 can be expressed in the form , where  and  are relatively prime positive integers. Find m + n.

Problem 11

In ∆ABC, the sides have integer lengths and AB = AC. Circle ω has its center at the incenter of ∆ABC. An excircle of 

∆ABC is a circle in the exterior of ∆ABC that is tangent to one side of the triangle and tangent to the extensions of the other two sides. Suppose that the excircle tangent to  is internally tangent to ω, and the other two excircles are both externally tangent to ω. Find the minimum possible value of the perimeter of ∆ABC.

Problem 12

Given f(z) = z2 - 19z , there are complex numbers z with the property that z, f(z), and f(f(z)) are the vertices of a right triangle in the complex plane with a right angle at f(z). There are positive integers m and n such that one such value of z is . Find m + n.

Problem 13

Triangle ABC has side lengths AB = 4, BC = 5, and CA = 6. Points D and E are on ray AB with AB < AD < AE. The point F ≠ C is a point of intersection of the circumcircles of 

ΔACD and  ΔEBC satisfying DF = 2 and EF = 7. Then BE can be expressed as , where a, b, c, and d are positive integers such that a and d are relatively prime, and c is not divisible by the square of any prime. Find a + b + c + d.

Problem 14

Find the least odd prime factor of 20198 + 1.

Problem 15

Let  be a chord of a circle ω, and let P be a point on the chord . Circle ω1 passes through A and P and is internally tangent to ω. Circle ω2 passes through B and P and is internally tangent to ω. Circles ω1 and ω2 intersect at points P and Q. Line PQ intersects ω at X and Y. Assume that AP = 5, PB = 3, XY = 11, and , where m and n are relatively prime positive integers. Find m + n.