2014年 AMC12 A卷

2014 AMC 12A Problems

$10 \cdot \left(\tfrac{1}{2} + \tfrac{1}{5} + \tfrac{1}{10}\right)^{-1}?$ Problem 1

What is

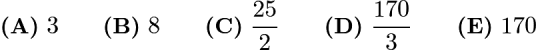
$\textbf{(A)}\ 3\qquad\textbf{(B)}\ 8\qquad\textbf{(C)}\ \frac{25}{2}\qquad\textbf{(D)}\ \frac{170}{3}\qquad\textbf{(E)}\ 170$

Problem 2

At the theater children get in for half price. The price for 5 adult tickets and 4 child tickets is 24.50. How much would 8 adult tickets and 6 child tickets cost?

$\textbf{(A) }35\qquad \textbf{(B) }38.50\qquad \textbf{(C) }40\qquad \textbf{(D) }42\qquad \textbf{(E) }42.50$

Problem 3

Walking down Jane Street, Ralph passed four houses in a row, each painted a different color. He passed the orange house before the red house, and he passed the blue house before the yellow house. The blue house was not next to the yellow house. How many orderings of the colored houses are possible?

$\textbf{(A)}\ 2\qquad\textbf{(B)}\ 3\qquad\textbf{(C)}\ 4\qquad\textbf{(D)}\ 5\qquad\textbf{(E)}\ 6$

Problem 4

Suppose that a cows give b gallons of milk in c days. At this rate, how many gallons of milk will d cows give in e days?

$\textbf{(A)}\ \frac{bde}{ac}\qquad\textbf{(B)}\ \frac{ac}{bde}\qquad\textbf{(C)}\ \frac{abde}{c}\qquad\textbf{(D)}\ \frac{bcde}{a}\qquad\textbf{(E)}\ \frac{abc}{de}$

Problem 5

On an algebra quiz, 10% of the students scored 70 points, 35% scored 80 points, 30% scored 90 points, and the rest scored 100 points. What is the difference between the mean and median score of the students' scores on this quiz?

$\textbf{(A)}\ 1\qquad\textbf{(B)}\ 2\qquad\textbf{(C)}\ 3\qquad\textbf{(D)}\ 4\qquad\textbf{(E)}\ 5$

Problem 6

The difference between a two-digit number and the number obtained by reversing its digits is 5 times the sum of the digits of either number. What is the sum of the two digit number and its reverse?

$\textbf{(A) }44\qquad \textbf{(B) }55\qquad \textbf{(C) }77\qquad \textbf{(D) }99\qquad \textbf{(E) }110$

Problem 7

The first three terms of a geometric progression are , and . What is the fourth term?

$\textbf{(A) }1\qquad \textbf{(B) }\sqrt[7]3\qquad \textbf{(C) }\sqrt[8]3\qquad \textbf{(D) }\sqrt[9]3\qquad \textbf{(E) }\sqrt[10]3\qquad$

Problem 8

A customer who intends to purchase an appliance has three coupons, only one of which may be used:

Coupon 1 : 10% off the listed price if the listed price is at least 50

Coupon 2: 20 dollars off the listed price if the listed price is at least 100

Coupon 3: 18% off the amount by which the listed price exceeds 100

For which of the following listed prices will coupon 1 offer a greater price reduction than either coupon 2 or coupon 3?

$\textbf{(A) }179.95\qquad \textbf{(B) }199.95\qquad \textbf{(C) }219.95\qquad \textbf{(D) }239.95\qquad \textbf{(E) }259.95\qquad$

Problem 9

Five positive consecutive integers starting with a have average b. What is the average of 5 consecutive integers that start with b?

$\textbf{(A)}\ a+3\qquad\textbf{(B)}\ a+4\qquad\textbf{(C)}\ a+5\qquad\textbf{(D)}\ a+6\qquad\textbf{(E)}\ a+7$

Problem 10

Three congruent isosceles triangles are constructed with their bases on the sides of an equilateral triangle of side length 1. The sum of the areas of the three isosceles triangles is the same as the area of the equilateral triangle. What is the length of one of the two congruent sides of one of the isosceles triangles?

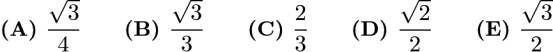
$\textbf{(A) }\dfrac{\sqrt3}4\qquad \textbf{(B) }\dfrac{\sqrt3}3\qquad \textbf{(C) }\dfrac23\qquad \textbf{(D) }\dfrac{\sqrt2}2\qquad \textbf{(E) }\dfrac{\sqrt3}2$

Problem 11

David drives from his home to the airport to catch a flight. He drives 35 miles in the first hour, but realizes that he will be 1 hour late if he continues at this speed. He increases his speed by 15 miles per hour for the rest of the way to the airport and arrives 30 minutes early. How many miles is the airport from his home?

$\textbf{(A) }140\qquad \textbf{(B) }175\qquad \textbf{(C) }210\qquad \textbf{(D) }245\qquad \textbf{(E) }280\qquad$

Problem 12

Two circles intersect at points A and B. The minor arcs AB measure 30° on one circle and 60° on the other circle. What is the ratio of the area of the larger circle to the area of the smaller circle?

$\textbf{(A) }2\qquad \textbf{(B) }1+\sqrt3\qquad \textbf{(C) }3\qquad \textbf{(D) }2+\sqrt3\qquad \textbf{(E) }4\qquad$

Problem 13

A fancy bed and breakfast inn has 5 rooms, each with a distinctive color-coded decor. One day 5 friends arrive to spend the night. There are no other guests that night. The friends can room in any combination they wish, but with no more than 2 friends per room. In how many ways can the innkeeper assign the guests to the rooms?

$\textbf{(A) }2100\qquad \textbf{(B) }2220\qquad \textbf{(C) }3000\qquad \textbf{(D) }3120\qquad \textbf{(E) }3125\qquad$

Problem 14

Let a < b < c be three integers such that a, b, c, is an arithmetic progression and a, c, b is a geometric progression. What is the smallest possible value of c?

$\textbf{(A) }-2\qquad \textbf{(B) }1\qquad \textbf{(C) }2\qquad \textbf{(D) }4\qquad \textbf{(E) }6\qquad$

Problem 15

A five-digit palindrome is a positive integer with respective digits abcba, where a is non-zero. Let S be the sum of all five-digit palindromes. What is the sum of the digits of S?

$\textbf{(A) }9\qquad \textbf{(B) }18\qquad \textbf{(C) }27\qquad \textbf{(D) }36\qquad \textbf{(E) }45\qquad$

Problem 16

The product (8)(888...8), where the second factor has k digits, is an integer whose digits have a sum of 1000. What is k?

$\textbf{(A) }901\qquad \textbf{(B) }911\qquad \textbf{(C) }919\qquad \textbf{(D) }991\qquad \textbf{(E) }999\qquad$

Problem 17

A 4 x 4 x h rectangular box contains a sphere of radius 2 and eight smaller spheres of radius 1. The smaller spheres are each tangent to three sides of the box, and the larger sphere is tangent to each of the smaller spheres. What is h?

$\textbf{(A) }2+2\sqrt 7\qquad \textbf{(B) }3+2\sqrt 5\qquad \textbf{(C) }4+2\sqrt 7\qquad \textbf{(D) }4\sqrt 5\qquad \textbf{(E) }4\sqrt 7\qquad$

Problem 18

The domain of the function $f(x)=\log_{\frac12}(\log_4(\log_{\frac14}(\log_{16}(\log_{\frac1{16}}x))))$ is an interval of length , where m and n are relatively prime positive integers. What is m + n?

$\textbf{(A) }19\qquad \textbf{(B) }31\qquad \textbf{(C) }271\qquad \textbf{(D) }319\qquad \textbf{(E) }511\qquad$

Problem 19

There are exactly N distinct rational numbers k such that |k| ， 200 and 5x2 + kx + 2 = 0 has at least one integer solution for x. What is N?

$\textbf{(A) }6\qquad \textbf{(B) }12\qquad \textbf{(C) }24\qquad \textbf{(D) }48\qquad \textbf{(E) }78\qquad$

Problem 20

In ∆BAC, ∠BAC = 40°, AB = 10, and AC = 6. Points D and E lie on $\overline{AB}$ and $\overline{AC}$ respectively. What is the minimum possible value of BE + DE + CD ?

$\textbf{(A) }6\sqrt 3+3\qquad \textbf{(B) }\dfrac{27}2\qquad \textbf{(C) }8\sqrt 3\qquad \textbf{(D) }14\qquad \textbf{(E) }3\sqrt 3+9\qquad$

Problem 21

For every real number x, let denote the greatest integer not exceeding x, and let . The set of all numbers x such that 1 ≤ x ≤ 2014 and f(x) ≤ 1 is a union of disjoint intervals. What is the sum of the lengths of those intervals?

$\textbf{(A) }1\qquad \textbf{(B) }\dfrac{\log 2015}{\log 2014}\qquad \textbf{(C) }\dfrac{\log 2014}{\log 2013}\qquad \textbf{(D) }\dfrac{2014}{2013}\qquad \textbf{(E) }2014^{\frac1{2014}}\qquad$

Problem 22

The number 5867 is between 22013 and 22014 . How many pairs of integers (m,n) are there such that 1 ≤ m ≤ 2012 and 5n < 2m < 2m+2 < 5n+1 ?

$\textbf{(A) }278\qquad \textbf{(B) }279\qquad \textbf{(C) }280\qquad \textbf{(D) }281\qquad \textbf{(E) }282\qquad$

Problem 23

The fraction , where n is the length of the period of the repeating decimal expansion. What is the sum b0 + b1 + ... + bn-1 ?

$\textbf{(A) }874\qquad \textbf{(B) }883\qquad \textbf{(C) }887\qquad \textbf{(D) }891\qquad \textbf{(E) }892\qquad$

Problem 24

Let f0(x) = x + |x - 100| - |x + 100|, and for n ≥ 1, let fn(x) = |fn-1(x)| - 1. For how many values of x is f100(x) = 0 ?

$\textbf{(A) }299\qquad \textbf{(B) }300\qquad \textbf{(C) }301\qquad \textbf{(D) }302\qquad \textbf{(E) }303\qquad$

Problem 25

The parabola P has focus (0,0) and goes through the points (4,3) and (-4,-3). For how many points (x,y) ∈P with integer coordinates is it true that |4x + 3y| ≤ 1000 ?